How Wheatstone Bridge will Work?
To find an unknown resistance in a circuit, the Wheatstone bridge is actively used. And it is very important to solve various types of problems and questions, that involve resistors, and other circuits. So, the students need to understand the workings of Wheatstone Bridge. Therefore, to help you out, here in the article below, we will provide a comprehensive description of Wheatstone Bridge.
Principle of Wheatstone Bridge
The Basic Principle of Wheatstone Bridge is the Principle of Null Deflection. According to this principle, there is no current present in this circuit, and the ratio of resistances is said to be the same. Moreover, at first, the bridge in the circuit, as shown in the diagram, exists in an unbalanced condition, and they can find the current is indeed flowing through the galvanometer. However, to keep the bridge in a balanced condition, there should not be any current flow in the circuit. However, to achieve this balanced position, it is needed to adjust the variable resistance and known resistance in the circuit.
Construction of Wheatstone Bridge
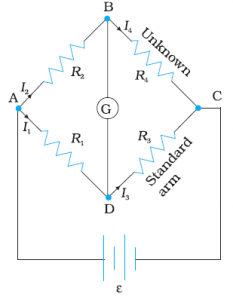
From the above diagram, as you can see, the Wheatstone Bridge consists of four arms, two known and two unknown resistances, and more importantly a variable resistance. The G symbol located in the center of the circuit represents Galvanometer. The emf source is attached to points a and c, while the galvanometer is connected between points b and d.
Wheatstone Bridge Formula Derivation
The currents I1 and i2 are divided into two equals in magnitude, because of the galvanometer. If the current in the galvanometer is considered zero, then,
\(I_{1}P= I_{2}R\)
In balanced condition, the terms and quantities in the balanced conditions are represented as,
\(I_{1}=I_{3}= \frac{E}{P+Q} \)
\(I_{2}=I_{4}= \frac{E}{R+S}\)
Where, E = emf of the battery, and
\(\frac{PE}{P+Q} =\frac{RE}{R+S}\)
\(\frac{E}{P+Q}=\frac{E}{R+S}\)
\(P(R+S)=R(P+Q)\)
\(PR+PS=PR+QR\)
\(PS=RQ\)
\(R= \frac{P}{Q}S\)
In this equation,
R = Unknown Resistance
S = Standard Arm of the Bridge
P/Q = Ratio Arm of Bridge
Applications of Wheatstone Bridge
- To measure the low resistance in a circuit.
- Other important quantities such as Capacitance, Impedance, and Inductance, can also be calculated using Wheatstone Bridge.
- By using an optional amplifier, in the Wheatstone bridge, we will be able to measure physical parameters like Strain, Light, and Temperature.
Limitations of Wheatstone Bridge
There are certain limitations to all types of principles in Physics, including the Wheatstone Bridge.
- Excessive current flow in the Wheatstone Bridge may result in a permanent change in the value of resistance.
- When low resistance is applied, leads and contacts in the circuit will cause an error, and their values will attain constant.
- In terms of high resistance, the measured values are off-charts, and then the galvanometer is considered to be in imbalance.
Conclusion
There are many other complex topics and chapters in Physics subject, which might need the students to put in some extra hard work to understand them easily and thoroughly. However, instead of self-study, we suggest students join online interactive classes. And if you are looking for a cost-effective online coaching program, with amazing benefits, then go check out the online tuition classes offered by the Tutoroot platform.
For more simplified explanations like the one above, visit the physics blogs on the Tutoroot website. Elevate your learning with Tutoroot’s personalised Physics online tuition classes. Begin your journey with a FREE DEMO session and discover the advantages of one-on-one online guidance.
Frequently Asked Questions
Which instrument is used as a null detector in Wheatstone Bridge?
The Galvanometer is the Null Detector in the Wheatstone Bridge.
What is the balanced condition of the Wheatstone Bridge?
The Balanced Condition in the Wheatstone bridge is observed when no current passes through the Galvonmeter.
