Complete List for Trigonometry Formulae & Identities 2024

Trigonometry is the study of triangles and connections between triangle lengths and angles in mathematics. Trigonometric formulas and a list of trigonometric identities form one of the most timeless and important facets of mathematics.

Trigonometry and related equations have a plethora of applications. Triangulation, for example, is used in Geography to calculate the distance between landmarks; in Astronomy they are used to determine the distance to neighboring stars; and, in satellite navigation systems. In many other ways, Trigonometric formulae are useful and indispensable too.

In this article, let us throw light on trigonometry formulas – inverse trigonometry formulas and basic trigonometry formulas.

Trigonometry Formulas

Trigonometry formulas are a collection that uses trigonometric identities to solve problems, involving the sides and angles of a right-angled triangle. For given angles, these trigonometry formulas include trigonometric functions such as sine, cosine, tangent, cosecant, secant, and cotangent. While the trigonometric formulae involving trigonometric identities are the core of the subject, we also would like to understand the importance of trigonometric identities, which in a basic sense refers to an equation that involves trigonometric ratios of an angle.

In the following sections, trigonometric identities, including Pythagorean identities, product identities, co-function identities (shifting angles), sum & difference identities, double-angle identities, half-angle identities, and so on are explained in detail.

List of Trigonometric Formulas

When we first learn about trigonometric formulas, we only consider right-angled triangles. As we know, a right-angled triangle has three sides: the hypotenuse, the opposite side (perpendicular), and the adjacent side (Base). The longest side in a right-angled triangle is known as the hypotenuse, the opposite side is perpendicular, and the adjacent side is where both the hypotenuse and the opposite side rest. These sides and the basic structure of the right-angled triangle go a long way in determining the depth of understanding of trigonometry formulae. In short, the right-angled triangle is the reference point to derive or arrive at trigonometry formulae or trigonometric identities.

Here is a list of trigonometry formulas.

• Basic Trigonometric Formulas 
• Inverse Trigonometric Formulas 
• Trigonometry Identities 
• Reciprocal Identities 
• Periodic Identities 
• Co-function Identities 
• Sum and Difference Identities 
• Double Angle Identities 
• Triple Angle Identities 
• Half Angle Identities 
• Product identities 
• Sum to Product Identities 

 Basic Trigonometric Formulas

In Trigonometry, there are six ratios that are utilized to find the elements. They are referred to as trigonometric functions. Sine, cosine, secant, cosecant, tangent, and cotangent are the six trigonometric functions.

As we understand that the trigonometric functions and identities are obtained using a right-angled triangle as a reference, this diagram gives a better picture for learning:

\(sin \theta = \frac{Opposite Side}{Hypotenuse}\)

\(cos \theta = \frac{Adjacent Side}{Hypotenuse}\)

\(tan \theta = \frac{Opposite Side}{Adjacent Side}\)

\(sec \theta = \frac{Hypotenuse}{Adjacent Side}\)

\(cosec \theta = \frac{Hypotenuse}{Opposite Side}\)

\(cot \theta = \frac{Adjacent Side}{Opposite Side}\)

Inverse Trigonometric Formulas

Trigonometric ratios are inverted using inverse trigonometry formulas to produce inverse trigonometric functions such as sin θ = x and \( \theta = sin^{-1}x\). In this case, x can take the form of whole integers, decimals, fractions, or exponents. 

\(sin^{-1}(-x)=- sin^{-1}x\)

\(cos^{-1}(-x)= \Pi -cos^{-1}x\)

\(tan^{-1}(-x)= – tan^{-1}x\)

\(cosec^{-1}(-x)= – cosec^{-1}x\)

\(sec^{-1}(-x)= \Pi -sec^{-1}x\)

\(cot^{-1}(-x)= \Pi -cot^{-1}x\)

Trigonometry Identities

Trigonometric Identities are equalities that involve trigonometry functions that stay valuable for all variables in the equation.

There are several trigonometric identities relating to the side length and angle of a triangle. These identities stay true to the right-angle triangle.

Reciprocal Identities

Trigonometric ratios feature reciprocal relation between a pair of ratios:

\(cosec \theta = \frac{1}{sin \theta }\)

\(sec \theta = \frac{1}{cos \theta }\)

\(cot \theta = \frac{1}{tan \theta }\)

\(sin \theta = \frac{1}{cosec \theta }\)

\(cos \theta = \frac{1}{sec \theta }\)

\(tan \theta = \frac{1}{cot \theta }\)

As explained, these are all derived from a right-angled triangle. If we know the height and base side of the right triangle, it will become easier to know sine, cosine, tangent, secant, cosecant, and cotangent values, by applying trigonometric formulas. We can also derive reciprocal trigonometric identities by applying trigonometric functions.

Periodicity Identities

The periodicity identities are formulas used to shift the angles by π/2, π, 2π, etc. They are also classified under cofunction identities.

• sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
• sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
• sin (3π/2 – A)  = – cos A & cos (3π/2 – A)  = – sin A
• sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
• sin (π – A) = sin A &  cos (π – A) = – cos A
• sin (π + A) = – sin A & cos (π + A) = – cos A
• sin (2π – A) = – sin A & cos (2π – A) = cos A
• sin (2π + A) = sin A & cos (2π + A) = cos A

If one observes keenly, fundamentally, all trigonometric identities are cyclic. They repeat after this periodicity constant. The periodicity constant varies among the trigonometric identities and is different for each.

Co-function Identities

\(sin(90^{0} -x)=cosx\)

\(cos(90^{0} -x)=sinx\)

\(tan(90^{0} -x)=cotx\)

\(cot(90^{0} -x)=tanx\)

\(sec(90^{0} -x)=cosecx\)

\(cosec(90^{0} -x)=secx\)

Trigonometric Identities of Opposite Angles

As we dwell deep into trigonometry formulas and various other aspects of this branch of mathematics, we explore more interesting features that enhance our subject knowledge and take us through new paths of knowledge. One such is the trigonometric identities of opposite angles, where, a trigonometry angle that is measured in its clockwise direction, is measured in negative parity. The trigonometric ratios for the angle’s negative parity are as follows:

• sin (-θ) = -sin θ
• cos (-θ) = cos θ
• tan (-θ) = -tan θ
• cot (-θ) = -cot θ
• sec (-θ) = sec θ
• cosec (-θ) = -cosec θ

Complementary Angles Identities

As the expression suggests, complementary angles are the pair of angles whose added measure comes to 90°. Their trigonometric identities are:

• sin (90° – θ) = cos θ
• cos (90° – θ) = sin θ
• tan (90° – θ) = cot θ
• cot ( 90° – θ) = tan θ
• sec (90° – θ) = cosec θ
• cosec (90° – θ) = sec θ

Supplementary Angles Identities

These are a pair of angles whose measure adds to 180°. Their trigonometric identities are:

• sin (180°- θ) = sinθ
• cos (180°- θ) = -cos θ
• cosec (180°- θ) = cosec θ
• sec (180°- θ)= -sec θ
• tan (180°- θ) = -tan θ
• cot (180°- θ) = -cot θ

Periodicity of Trigonometric Function

Trigonometric functions, sin, cos, tan, cot, sec, and cosec, are all periodic and carry different periodicities. Their identities:

• sin (n × 360° + θ) = sin θ
• sin (2nπ + θ) = sin θ
• cos (n × 360° + θ) = cos θ
• cos (2nπ + θ) = cos θ
• tan (n × 180° + θ) = tan θ
• tan (nπ + θ) = tan θ
• cosec (n × 360° + θ) = cosec θ
• cosec (2nπ + θ) = cosec θ
• sec (n × 360° + θ) = sec θ
• sec (2nπ + θ) = sec θ
• cot (n × 180° + θ) = cot θ
• cot (nπ + θ) = cot θ

Where, n ∈ Z, (Z = set of all integers)

Note: sin, cos, cosec, and sec have a period of 360° or 2π radians, and for tan and cot period is 180° or π radians.

Sum and Difference Identities

Double Angle Identities

Triple Angle Identities

Half Angle Identities

Product identities

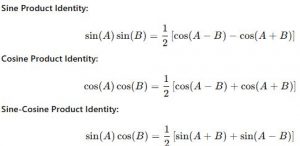
Sum to Product Identities

 

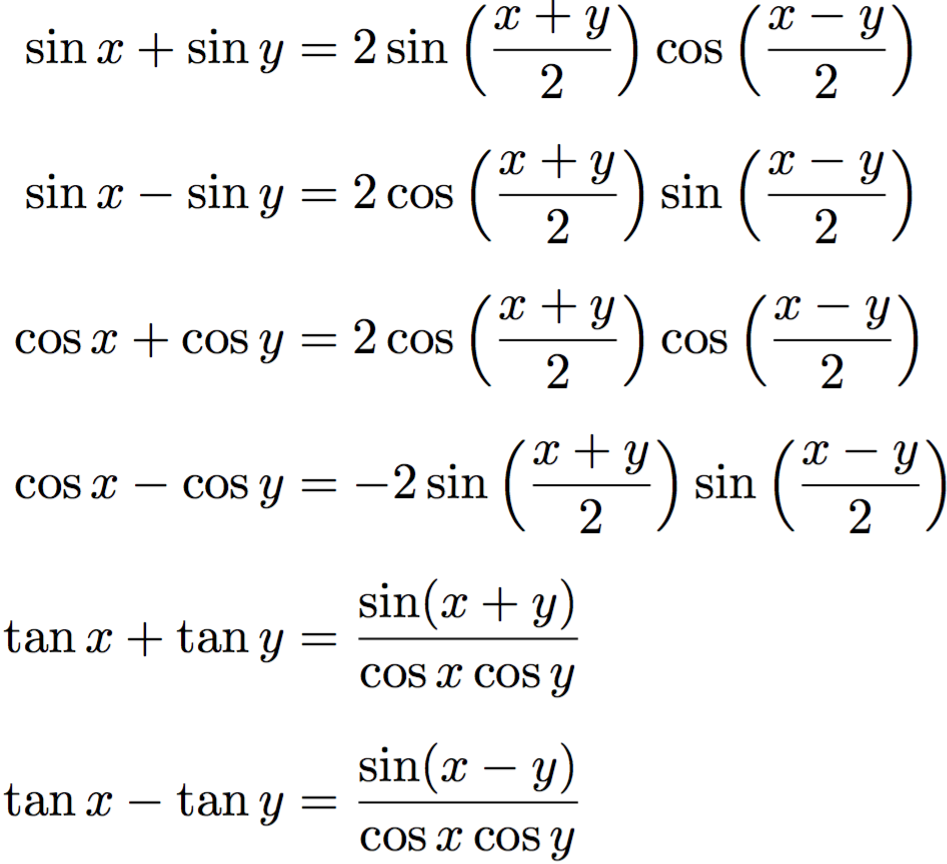
Final Notes

In this article, we tried to capture the list of Trigonometry Formulas. These formulae are useful for solving problems based chiefly on trigonometry. In addition to them, trigonometric identities help you develop Trigonometric Formulas.

At  Tutoroot, we offer personalized trigonometry tutoring to ensure a clear understanding. Our expert instructors use simple teaching approaches for an effective understanding of the subject. Sign up with Tutoroot’s Online Tuition for Maths to learn more.

FAQs

What are the 4 types of trigonometry?

Core, plane, spherical and analytic

What is sin theta?

Sin theta is a trigonometry function. In a right-angled triangle, it is the ratio of the opposite side to the hypotenuse of the triangle

What is cos theta?

Cos theta is the ratio of the base to the hypotenuse of the right-angle triangle

What is tan theta?

Also referred to as the law of tangent, tan theta is the ratio of the opposite side of a triangle to the adjacent side. It can also the ratio of the sine of the angle to its cosine