What are Adiabatic Process and Isothermal Process?

Introduction to Isothermal Process and Adiabatic Process

In the world of thermodynamics, two crucial processes play a significant role in understanding the behavior of gases: the isothermal process and the adiabatic process. These processes go hand in hand, yet possess distinct characteristics and implications. Understanding their fundamental principles can pave the way for a deeper comprehension of energy transfer and transformation. In this comprehensive guide, we will delve into the essence of both processes, explore their equations, highlight their real-life applications, and distinguish the variances between them. 

What is Adiabatic Process?

An adiabatic process is characterized by its ability to occur without any heat exchange between the system and its surroundings. In other words, during an adiabatic process, there is neither heat gained nor lost from the system. This implies that the change in internal energy solely depends on the work done on or by the system. The absence of heat transfer allows us to witness fascinating phenomena, where the temperature and pressure of the gas vary considerably without any corresponding exchange of thermal energy. 

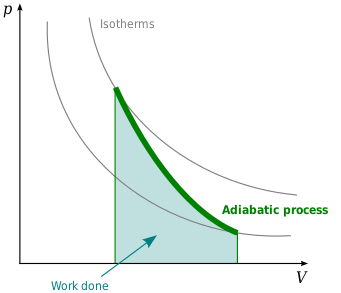
It sounds confusing, let’s understand it in simple way now. An adiabatic process is a thermodynamic process in which there is no exchange of heat with the surroundings. In simpler terms, it’s a process where the heat energy within a system remains constant. During an adiabatic process, the internal energy of the system can change, but there is no heat transfer in or out. 

Adiabatic Process Examples

To better comprehend the concept of an adiabatic process, we have a look at the examples of Adiabatic process. 

• Imagine a gas being compressed suddenly, such as when a tire is rapidly inflated. In this scenario, the gas molecules experience an increase in pressure and temperature due to the compression, without any heat being added. Conversely, if the gas expands suddenly, perhaps by releasing it from a pressurized container, the pressure and temperature of the gas decrease sharply without any heat loss. 
• Another instance of an adiabatic process is the ascent of a weather balloon. As the balloon rises through the Earth’s atmosphere, the external pressure decreases rapidly, causing the air inside the balloon to expand adiabatically. This expansion results in a cooling effect, which is why the air inside the balloon becomes colder at higher altitudes. 

Adiabatic Process Equation

In mathematical terms, the relationship between pressure (P) and volume (V) during an adiabatic process is given by the adiabatic equation: 

\(P V^{ \gamma } =constant\)

\(\gamma\) is the ratio of specific heats \((\frac{ C_{p} }{ C_{v} })\)

P is the Pressure of the Gas,

V is the volume of the Gas

where γ represents the heat capacity ratio or the adiabatic index. This ratio is specific to the gas involved in the process. For example, for monatomic ideal gases like helium or argon, the value of γ is approximately 5/3, whereas for diatomic gases like nitrogen or oxygen, the value is around 7/5. 

This equation allows us to quantify the variations in pressure and volume experienced by a gas undergoing an adiabatic process. By comparing the initial and final states of the system, we can calculate the change in pressure and volume. 

Work Done in Adiabatic Process

The work done during an adiabatic process can be determined by integrating the pressure-volume relationship. Since the adiabatic equation relates pressure and volume, we can rearrange it to solve for pressure:

\(p= \frac{Constant}{ V^{ \gamma } } \)

By substituting this expression for pressure into the work formula, we can calculate the work done during an adiabatic process. The resulting integral depends on the specific boundaries of the system and provides valuable insights into the energy transformations occurring. 

\(W= \frac{ P_{1} V_{1} – P_{2} V_{2} }{1- \gamma }\)

Where W is the work done

What is Adiabatic Change? 

Adiabatic change refers to the alteration of a system’s parameters without any heat exchange, maintaining constant entropy. While this may seem complex, it simply means that during an adiabatic change, the energy within the system does not transfer through heat, leaving the entropy (a measure of disorder) unaffected. 

What is Reverse Adiabatic Process? 

A reverse adiabatic process, commonly referred to as an isentropic process, is the opposite of an adiabatic process. It occurs when a system undergoes change while maintaining constant entropy. In a reverse adiabatic process, the energy transfer occurs only through heat, while the entropy remains constant. 

What is the Isothermal Process?

Unlike an adiabatic process, an isothermal process is characterized by maintaining a constant temperature throughout the entire process. In simple terms, during an isothermal process, heat is continuously exchanged between the system and its surroundings to maintain a stable temperature. This implies that any change in pressure or volume results solely from the transfer of thermal energy. 

Isothermal Process Equation 

The relationship between pressure and volume during an isothermal process is given by Boyle’s law. According to this law, the pressure and volume of a given amount of gas are inversely proportional at a constant temperature. Mathematically, it can be expressed as: 

\(P_{1} V_{1} = P_{2} V_{2}\)

where P1 and P2 are the initial and final pressures, and V1 and V2 are the initial and final volumes. 

Work Done in Isothermal Process 

During an isothermal process, the work done can be determined using the following equation:

\(W=nRT ln( \frac{ V_{2} }{ V_{1} } )\)

where W represents the work done, n is the number of moles of gas, R is the ideal gas constant, T is the temperature, and V1 and V2 denote the initial and final volumes, respectively. 

Isothermal Process Examples 

The Examples of isothermal processes are given below,

• Imagine a gas confined within a cylinder being heated or cooled while the piston remains immovable. In this scenario, the temperature of the gas is maintained at a constant value, allowing us to observe changes in pressure and volume due to the addition or removal of thermal energy. 
• Another example of an isothermal process is seen in refrigeration systems. These systems utilize the principle of heat exchange to cool a space or preserve perishable goods. By compressing gas and then allowing it to expand while absorbing heat, refrigeration systems can maintain a constant temperature throughout the process, ensuring efficient cooling. 

What is Boyle’s Law? 

Boyle’s law states that at a constant temperature, the pressure and volume of a gas are inversely proportional to each other. Essentially, as the volume of a gas decreases, its pressure increases, and vice versa, as long as the temperature remains constant. 

Boyle’s Law Equation

Boyle’s law can be mathematically expressed as: 

\(P_{1} V_{1} = P_{2} V_{2}\)

or

\(PV=nRT\)

where P1 and P2 represent the initial and final pressures, and V1 and V2 denote the initial and final volumes, respectively. This equation succinctly captures the relationship between pressure and volume in an isothermal process. 

Importance of Boyle’s Law 

Boyle’s law has significant implications across various fields, especially in the study of gases. It aids in understanding gas behavior, predicting volume changes resulting from pressure alterations, and ensuring the efficiency of devices like compressors, engines, and refrigerators. By quantifying the relationship between pressure and volume, Boyle’s law helps engineers and scientists design systems that function optimally. 

Difference Between Isothermal Process and Adiabatic Process

The distinguish between isothermal and adiabatic processes are described below, 

Aspect	Isothermal Process	Adiabatic Process
Heat Exchange	Heat exchange occurs with surroundings to maintain a constant temperature.	No heat exchange with surroundings; temperature may change.
Temperature	Temperature remains constant throughout the process.	Temperature can change during the process.
Work Done Equation	\(W=nRT ln( \frac{ V_{2} }{ V_{1} } )\)	\(W= \frac{ P_{1} V_{1} – P_{2} V_{2} }{1- \gamma }\)
Equation Type	Follows the ideal gas law  \(PV=nRT\)	Follows the equation  \(P V^{ \gamma } =constant\)
Applications	Often observed in refrigeration and ideal gas behavior.	Commonly seen in rapid compression and expansion situations, such as in engines.
Example	Cooling of a can of compressed air when sprayed.	Compression of air inside a bicycle tire when pumped.

These are the major differences between isothermal and adiabatic processes 

Final Notes

Understanding the nuances of isothermal and adiabatic processes provides a foundation for comprehending the behavior, transformations, and energy transfers within gases. While both processes involve gas expansion and compression, their distinct characteristics, such as heat exchange and temperature variation, set them apart. By leveraging the equations and concepts discussed in this guide, one can better analyze and predict the behavior of gases under different thermodynamic scenarios. 

This is in-depth information about the adiabatic process and isothermal process, Hope this article clears all information about the difference between the adiabatic process and the isothermal process, Boyle’s law, importance of Boyle’s law. Tutoroot offers one-on-one tuition for all the classes to various boards and exams. If you want to experience our interactive online classes, you can book a FREE DEMO now by just clicking here. 

FAQs

What is an adiabatic process?

An adiabatic process refers to a thermodynamic process occurring without any heat exchange between the system and its surroundings. The change in the system’s internal energy solely relies on the work done. 

Can you provide an example of an adiabatic process?

Certainly! One example of an adiabatic process is the sudden compression or expansion of a gas, such as a tire being inflated rapidly or releasing gas from a pressurized container. These processes result in a notable change in pressure and temperature without any heat transfer. 

What is the formula for adiabatic processes?

The relationship between pressure and volume during an adiabatic process is given by the adiabatic equation: \([latex]P V^{ \gamma } =constant\)[/latex] = constant, where γ represents the heat capacity ratio or the adiabatic index specific to the gas involved. 

What is the constant in an adiabatic process?

The constant in the adiabatic process equation depends on the initial and final states of the system and the specific boundaries within which the process occurs. It is determined based on the pressure-volume relationship and can vary for different systems and processes.