What are Oscillations and Why Do They Matter?

Introduction to Oscillations 

Oscillations are an inherent part of the physical world, from the motion of a simple pendulum to the vibrations of atoms in a solid. Defined as a repetitive back-and-forth motion around an equilibrium point, oscillations are fundamental to understanding various natural and man-made phenomena. This blog explores oscillations in detail, delving into their principles, mathematical representations, and applications. 

Periodic and Oscillatory Motion 

Periodic motion is any motion that repeats itself at regular intervals, such as the Earth’s orbit around the Sun. Oscillatory motion, a subset of periodic motion, involves an object moving to and fro about a fixed point or position. Examples include the swinging of a pendulum and the vibrations of a tuning fork. 

Key characteristics include: 

• Period (T): Time for one complete cycle. 
• Frequency (f): Number of cycles per second. 

Simple Harmonic Motion (SHM) 

SHM is a type of oscillatory motion where the restoring force is directly proportional to displacement and acts in the opposite direction. It is mathematically expressed as: 

Here, k is the spring constant, and xxx is the displacement from equilibrium. 

Conditions for SHM 

For motion to qualify as SHM, the following criteria must be met: 

• A restoring force exists, proportional to the displacement. 
• The system is frictionless or minimally damped. 
• Displacement remains small. 

Equation of Motion in SHM 

The displacement of a particle undergoing SHM is described by: 

Where: 

• A: Amplitude
• ω: Angular frequency
• ϕ: Phase constant

Velocity and acceleration are given by derivatives of displacement, showcasing a sinusoidal relationship. 

Energy in Simple Harmonic Motion 

SHM demonstrates the continuous exchange between kinetic energy (KE) and potential energy (PE): 

The total energy remains constant: 

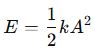
Damping and Damped Oscillations 

In real systems, friction and resistance reduce the amplitude of oscillations over time, leading to damped oscillations. 

• Underdamped: Oscillations decay gradually. 
• Critically damped: Returns to equilibrium without oscillating. 
• Overdamped: Returns slowly without oscillating. 

Forced Oscillations and Resonance 

When an external periodic force drives an oscillatory system, it undergoes forced oscillations. At certain frequencies, the amplitude of motion increases significantly, a phenomenon known as resonance. 

Example: Resonance in bridges and musical instruments. 

Examples of Oscillatory Systems 

• Pendulums

A simple pendulum, consisting of a mass suspended by a string, exhibits SHM for small angles. The motion is governed by:

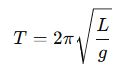
• Springs and Mass Systems

The spring-mass system is a classic SHM example, obeying Hooke’s Law:

Characteristics of SHM 

Amplitude, Frequency, and Period

• Amplitude (A): Maximum displacement from equilibrium.
• Frequency (f): Inversely proportional to the period (f=1/T).
• Period (T): Time for one oscillation.

Phase and Phase Difference

The phase (ϕ) represents the motion’s initial position, while the phase difference indicates the relative position between two oscillations.

Applications of Oscillations 

• Clocks

Pendulum clocks and quartz watches rely on oscillations for precise timekeeping.

• Engineering Systems

Oscillatory systems are crucial in designing bridges, suspension systems, and earthquake-resistant structures.

• Natural Phenomena

Examples include sound waves, seismic waves, and biological rhythms like the heartbeat.

Oscillations in Mechanical Systems 

Mechanical oscillations occur in coupled systems, such as coupled pendulums and vibrating beams. These systems exhibit complex interactions, leading to phenomena like normal modes.

Wave-Particle Connection in Oscillations 

Oscillations are foundational to understanding wave-particle duality in quantum mechanics, where particles exhibit wave-like behaviours, including oscillatory properties like frequency and wavelength. 

Energy Transfers in Oscillatory Motion 

Energy in oscillatory motion alternates between potential and kinetic forms. In damped systems, energy dissipates as heat, while in forced systems, energy input sustains motion. 

Mathematical Representation of Oscillations 

Oscillations are described by sinusoidal functions: 

Differential equations govern the behaviour of oscillatory systems, providing insights into their dynamics. 

Graphs of SHM: Displacement, Velocity, and Acceleration 

• Displacement (x): A cosine wave. 
• Velocity (v): A sine wave, phase-shifted by π/2. 
• Acceleration (a): A cosine wave, inverted and proportional to displacement. 

Comparison Between Oscillatory and Wave Motion 

While oscillatory motion is confined to a point, wave motion involves energy propagation through a medium. Waves are often generated by oscillatory systems, forming a deep connection between the two. 

Conclusion

Oscillations are not merely an academic concept; they underpin many technologies and natural processes. From timekeeping to seismic safety and quantum mechanics, understanding oscillations enriches our ability to innovate and comprehend the world around us. Whether in the swing of a pendulum or the vibrations of molecules, oscillations are a cornerstone of science and technology. 

If you’re looking to deepen your understanding of oscillatory motion or excel in physics, platforms like Tutoroot offer personalised learning and expert guidance. With interactive tools and tailored content, Tutoroot ensures you grasp even the most complex topics with ease. For a deeper understanding and personalised guidance in your studies, take advantage of Tutoroot’s Physics online tuition.