What is Quadrilaterals? Types, Properties, and Uses

Quadrilaterals are a fundamental concept in geometry that forms the basis of many shapes and figures we encounter in mathematics and the real world. From the tiles on our floors to the designs of buildings and bridges, quadrilaterals play an essential role. This in-depth blog will explore quadrilaterals in detail, including their definition, classification, properties, applications, and practical tips to master them. By the end of this guide, you will have a solid understanding of quadrilaterals and how they connect theory to practice.
What is a Quadrilateral?
In mathematics, a quadrilateral is a polygon with four sides, four angles, and four vertices. The term is derived from Latin: quadri- meaning “four” and latus meaning “side.” Quadrilaterals are two-dimensional shapes, and the sum of their internal angles is always 360 degrees. This property makes quadrilaterals a crucial part of many geometry problems.
While they may appear simple, quadrilaterals come in many different types, each with distinct properties that make them interesting to study and apply in real-world scenarios.
Types of Quadrilaterals
Quadrilaterals can be classified based on their sides, angles, and symmetry. Below is an overview of the major types.
1. Parallelogram
A parallelogram is a quadrilateral where opposite sides are parallel and equal in length.
Key Properties:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- Diagonals bisect each other.
- Adjacent angles are supplementary (sum to 180 degrees).
Examples: Rhombus, rectangle, and square.
Applications: Parallelograms are common in engineering and architecture, especially in trusses used in bridge designs.
2. Rectangle
A rectangle is a parallelogram with four right angles.
Key Properties:
- Opposite sides are equal and parallel.
- All four angles are 90 degrees.
- Diagonals are equal and bisect each other.
Formulae:
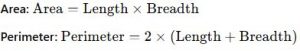
Applications: Rectangles are widely used in architecture (doors, windows, rooms) and technology (TVs, smartphones, and computer screens).
3. Square
A square is a special type of rectangle where all four sides are equal in length, and all angles are 90 degrees.
Key Properties:
- All sides are equal.
- All four angles are 90 degrees.
- Diagonals are equal and intersect at right angles.
Formulae:
Applications: Squares appear in tiled floors, checkerboards, and even city planning (e.g., grids of square blocks).
4. Rhombus
A rhombus is a parallelogram where all sides are equal in length, but the angles are not necessarily 90 degrees.
Key Properties:
- All sides are equal.
- Opposite angles are equal.
- Diagonals bisect each other at right angles.
Formulae:
Applications: Rhombuses are found in design patterns, art, and even certain jewelry shapes.
5. Trapezium (Trapezoid)
A trapezium has one pair of parallel opposite sides.
Key Properties:
- One pair of opposite sides (called bases) is parallel.
- Non-parallel sides are known as legs.
- The angles adjacent to each base are supplementary.
Formulae:
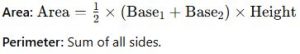
Applications: Trapeziums are used in designing sloping roofs, car ramps, and certain bridge components.
6. Kite
A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal.
Key Properties:
- One pair of opposite angles is equal.
- Diagonals intersect at right angles.
- One diagonal bisects the other.
Formulae:
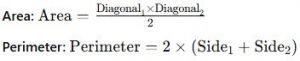
Applications: Kites are used not only as flying toys but also in aerodynamics and decorative art.
Properties of Quadrilaterals
Below is a summary of the key properties of different quadrilaterals:
| Quadrilateral | Parallel Sides | Equal Angles | Diagonals | Special Property |
| Parallelogram | 2 pairs | Opposite | Bisect each other | Opposite sides equal |
| Rectangle | 2 pairs | All 90 degrees | Equal | All angles right angles |
| Square | 2 pairs | All 90 degrees | Equal, bisect at right angles | All sides equal |
| Rhombus | 2 pairs | Opposite | Bisect at right angles | All sides equal |
| Trapezium | 1 pair | Adjacent supplementary | None | One pair of parallel sides |
| Kite | None | One pair | Intersect at right angles | Two pairs of adjacent sides equal |
Applications of Quadrilaterals in Real Life
Quadrilaterals are not just abstract mathematical concepts—they are everywhere around us. Below are some areas where quadrilaterals are used extensively:
- Architecture and Design
- Rectangles and squares are used in floor plans, wall designs, and windows.
- Trapeziums are used in bridges and sloping roofs.
- Parallelograms are found in trusses and frames to distribute loads efficiently.
- Graphic Design and Visual Arts
- Mosaics and tiling patterns use quadrilateral shapes to create artistic effects.
- Kites are often used in patterns and decorative ornaments.
- Technology
- Screens of TVs, laptops, and smartphones are rectangular for ergonomic reasons.
- User interfaces in apps and software are designed using grids made of quadrilateral sections.
- Sports and Games
- Fields and courts (like those in soccer and tennis) are rectangular.
- Checkerboards and chessboards use square grids for play.
Challenges Faced by Students in Learning Quadrilaterals
- Memorization of Properties:
With multiple types of quadrilaterals, students often struggle to remember all the properties and formulas.
- Visual Confusion:
Similar-looking shapes (like rhombuses and squares) can be confusing for beginners.
- Application-Based Problems:
Applying theoretical knowledge of quadrilaterals to solve practical problems requires practice.
Tips for Mastering Quadrilaterals
- Practice Drawing and Labeling:
Drawing the shapes helps reinforce memory and makes it easier to understand their properties.
- Solve Real-Life Problems:
Apply the knowledge of quadrilaterals to measure rooms, design layouts, or analyze patterns around you.
- Use Interactive Tools:
Geometry apps like GeoGebra allow students to visualize and manipulate quadrilaterals, deepening understanding.
- Break Down Complex Problems:
Divide word problems into smaller parts to identify which type of quadrilateral is being used.
Conclusion
Quadrilaterals are a vital part of geometry, forming the foundation for understanding shapes, design, and structures in the real world. By mastering the properties and applications of different quadrilateral types—such as squares, rectangles, and parallelograms—students gain essential problem-solving skills. These skills are not only useful in academics but also in fields like architecture, technology, and engineering.
For students looking to excel in mathematics and geometry, Tutoroot offers personalised online guidance. With expert tutors and interactive lessons, students can develop a strong grasp of complex topics like quadrilaterals. Understanding these shapes will not only help with exams but also enhance spatial awareness and logical thinking. With practice and the right resources, anyone can master quadrilaterals and enjoy learning geometry!
FAQ’s
How is a parallelogram different from a rectangle?
Both parallelograms and rectangles have opposite sides that are equal and parallel. However, a rectangle has all four angles as right angles (90 degrees), whereas the angles in a parallelogram are not necessarily 90 degrees.
What is the difference between a square and a rhombus?
- Square: All four sides are equal, and all angles are 90 degrees.
- Rhombus: All four sides are equal, but the angles are not necessarily 90 degrees. A rhombus is a type of parallelogram.
What is the area of a trapezium?
The formula for the area of a trapezium (or trapezoid) is:
where Base 1 and Base 2 are the lengths of the two parallel sides, and Height is the perpendicular distance between them.
How do you find the sum of the interior angles of a quadrilateral?
The sum of the interior angles of any quadrilateral is always 360 degrees. This is a key property that holds true for all types of quadrilaterals.
What are the properties of a kite?
A kite has:
- Two distinct pairs of adjacent sides that are equal.
- One pair of opposite angles that are equal.
- Diagonals that intersect at right angles, with one diagonal bisecting the other.
What makes a trapezium unique?
A trapezium (trapezoid in American English) is unique because it has only one pair of parallel sides, unlike other quadrilaterals such as parallelograms, which have two pairs of parallel sides.
Are all rectangles also parallelograms?
Yes, all rectangles are parallelograms because they have two pairs of opposite sides that are equal and parallel. However, not all parallelograms are rectangles since a parallelogram’s angles may not be 90 degrees.
Can a quadrilateral have all sides and angles different?
Yes, a general quadrilateral (an irregular quadrilateral) can have all four sides and all four angles different. It has no specific properties like those of parallelograms, rectangles, or squares.
What is the relationship between a square and a rectangle?
A square is a special type of rectangle where all four sides are equal. In other words, every square is a rectangle, but not every rectangle is a square.
How do you calculate the perimeter of a quadrilateral?
The perimeter of a quadrilateral is the sum of the lengths of all four sides. The formula can vary depending on the type of quadrilateral, but in general:
Are diagonals always equal in a quadrilateral?
No, diagonals are not always equal in all quadrilaterals. For example:
- In a rectangle and square, the diagonals are equal.
- In a rhombus and parallelogram, the diagonals are unequal, but they bisect each other.
- In a kite, one diagonal is longer and bisects the shorter one.
How can quadrilaterals be used in real life?
Quadrilaterals appear in many real-world applications, including:
- Architecture and construction (floors, walls, windows, and roofs)
- Design and engineering (trusses, bridges, and frames)
- Technology (screens of TVs, laptops, and phones)
- Games (chessboards and playing fields)
Why is the study of quadrilaterals important?
Understanding quadrilaterals helps build spatial awareness and problem-solving skills. It lays the foundation for higher geometry, which is essential in fields like engineering, architecture, art, and technology.
What are supplementary angles in a quadrilateral?
Supplementary angles are two angles whose sum is 180 degrees. In a parallelogram, the adjacent angles are supplementary, meaning they add up to 180 degrees.
Can a quadrilateral be both a kite and a rhombus?
Yes, a rhombus is a special type of kite where all sides are equal. However, not all kites are rhombuses since a kite only requires two pairs of adjacent sides to be equal, not all four sides.
How do you differentiate between a parallelogram and a rhombus?
Both parallelograms and rhombuses have parallel opposite sides. However:
- In a rhombus, all sides are equal, but the angles are not necessarily 90 degrees.
- In a parallelogram, the sides are equal in pairs, but not all four sides need to be equal.


