What is Geometry? Exploring the Fascinating World of Shapes, Space, and Mathematical Principles

Geometry is one of the most fundamental branches of mathematics, concerned with shapes, sizes, angles, and spatial relationships. Its significance goes beyond the classroom, impacting fields such as architecture, engineering, computer graphics, robotics, astronomy, and even art. This in-depth blog explores the origins, types, essential concepts, applications, and real-world relevance of geometry. Whether you’re a student or an enthusiast, this article will walk you through the fascinating world of geometry.
What is Geometry?
Geometry is the mathematical study of spatial properties and relationships of objects, including points, lines, angles, and surfaces. It involves understanding the dimensions and measurements of objects, analyzing how they relate, and exploring their behavior under transformations.
The word “geometry” is derived from the Greek words geo (earth) and metron (measure), reflecting the subject’s origins in land measurement. Early civilizations used geometry to divide land, construct buildings, and map territories, giving rise to concepts that form the backbone of modern mathematics.
A Brief History of Geometry
The history of geometry dates to ancient times and spans several cultures. Key milestones include:
- Ancient Egypt and Babylon:
- The Egyptians used geometric principles to measure land after the Nile River floods.
- Babylonians applied geometry for agricultural planning and astronomy.
2. Greek Geometry:
- The Greeks formalized geometry through logical reasoning. Euclid, often referred to as the “father of geometry,” compiled existing knowledge in his book The Elements.
- Pythagoras discovered the relationship between the sides of right-angled triangles (Pythagoras’ theorem).
3. Indian Contributions:
- Ancient Indian mathematicians like Aryabhata and Brahmagupta contributed to the development of geometry, particularly in astronomy and trigonometry.
4. Non-Euclidean Geometry (18th-19th Century):
- Mathematicians like Gauss, Riemann, and Lobachevsky developed new forms of geometry, including hyperbolic and spherical geometry.
5. Modern Geometry:
- With the advent of computers, geometry has found applications in 3D modeling, graphics, artificial intelligence (AI), and space exploration.
Types of Geometry
Geometry can be divided into several branches, each with unique characteristics and applications:
- Euclidean Geometry
- This is the geometry taught in most schools, based on Euclid’s postulates. It deals with flat spaces and covers familiar concepts like points, lines, angles, and polygons.
- Examples: Angles in a triangle add up to 180°, and parallel lines never meet.
2. Non-Euclidean Geometry
- In contrast to Euclidean geometry, this branch deals with curved surfaces.
- Types:
- Spherical Geometry: Used to study shapes on a sphere’s surface (e.g., Earth).
- Hyperbolic Geometry: Deals with negatively curved surfaces (useful in complex networks and theoretical physics).
3. Coordinate Geometry
- Combines algebra and geometry to study shapes using a Cartesian plane (x-y coordinate system).
- Applications: Used to calculate distances, slopes, and areas of shapes plotted on a graph.
4. Analytic Geometry
Extends the concept of coordinate geometry to study curves and surfaces using equations.
5. Differential Geometry
- Uses calculus to study the properties of curves and surfaces.
- Applications: Used in physics, particularly in Einstein’s theory of relativity.
6. Fractal Geometry
- Studies complex patterns that are self-similar at different scales.
- Examples: Fractals are found in nature, such as in snowflakes, coastlines, and tree branches.
Key Concepts in Geometry
Below are the core principles and topics that students encounter when studying geometry:
- Points, Lines, and Angles
- Point: A location in space with no size or dimension.
- Line: A straight path extending infinitely in both directions.
- Angle: Formed when two lines meet at a point (vertex).
Types of Angles:
- Acute (< 90°), Right (90°), Obtuse (> 90°), Straight (180°).
- Polygons and their Properties
- Polygons are closed figures with straight sides. Examples include triangles, quadrilaterals, pentagons, and hexagons.
- Triangles: Classified based on sides (scalene, isosceles, equilateral) and angles (acute, right, obtuse).
- Quadrilaterals: Include squares, rectangles, parallelograms, and trapezoids.
- Circles
- Circle: A shape where every point on the curve is equidistant from the center.
- Key components include:
- Radius, diameter, circumference, arcs, and chords.
- Central and Inscribed Angles: Important properties used to study angles in a circle.
- Mensuration
- Mensuration deals with calculating the area, perimeter, surface area, and volume of 2D and 3D objects.
- Perimeter: Length around a shape.
- Area: Surface covered by a shape.
- Volume: Space occupied by a solid.
Examples:
- Area of a triangle:
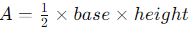
- Volume of a sphere:
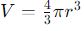
- Coordinate Geometry
- Plots point on a Cartesian plane using x and y coordinates.
- Distance Formula:
![]()
- Midpoint Formula:
![]()
- Transformations
- Transformations modify shapes through:
- Translation: Sliding a shape.
- Rotation: Turning a shape around a point.
- Reflection: Flipping a shape over a line.
- Scaling: Resizing a shape.
Applications of Geometry in the Real World
- Architecture and Engineering
- Architects use geometry to design buildings and ensure structural stability.
- Engineers apply geometry in constructing bridges, tunnels, and machinery.
2. Computer Graphics and Animation
3D models and virtual environments in video games and movies rely on geometric principles.
3. Astronomy and Space Science
Astronomers use geometry to calculate distances between celestial objects and model planetary orbits.
4. Robotics and AI
Robots need geometric algorithms to navigate spaces and perform tasks efficiently.
5. Art and Design
Artists use geometric patterns and symmetry to create visually appealing designs.
Importance of Geometry for Students
Studying geometry offers more than just academic knowledge—it cultivates essential life skills, including:
- Logical Reasoning: Students learn to think logically and build structured arguments.
- Spatial Awareness: Geometry helps in visualizing objects and understanding their relationships.
- Problem-Solving Skills: Geometric concepts encourage creative approaches to challenges.
Additionally, geometry forms the basis for advanced topics like trigonometry, calculus, and physics, making it essential for students pursuing careers in STEM fields.
Conclusion
Geometry is much more than a branch of mathematics; it’s a powerful tool that shapes how we see and interact with the world. From the design of towering skyscrapers to the precision of spacecraft trajectories, geometry is all around us. Mastering it not only enhances mathematical skills but also nurtures critical thinking, creativity, and problem-solving abilities.
For students looking to deepen their understanding of geometry, platforms like Tutoroot offer interactive and engaging lessons tailored to various academic levels. Geometry opens doors to exciting possibilities, inspiring learners to explore the beauty and logic underpinning the world. Tutoroot offers a comprehensive online maths tuition program designed to help students succeed. With experienced tutors, personalised learning plans, and a wealth of educational resources, Tutoroot provides the support and guidance students need to excel in maths.
FAQ’s
What are the basic elements of geometry?
The basic elements of geometry include:
- Point: Represents a position in space with no size or dimension.
- Line: A straight path that extends infinitely in both directions.
- Angle: Formed when two lines or rays meet at a point (vertex).
- Plane: A flat, two-dimensional surface that extends infinitely.
What is the difference between 2D and 3D geometry?
- 2D (Two-Dimensional) Geometry: Deals with flat shapes such as triangles, circles, and rectangles. These shapes have length and width but no depth (thickness).
- 3D (Three-Dimensional) Geometry: Focuses on solids like cubes, spheres, and cylinders, which have length, width, and height (or depth).
What are the most important theorems in geometry?
Some key theorems in geometry include:
- Pythagoras’ Theorem: In a right-angled triangle, a2+b2=c2a^2 + b^2 = c^2a2+b2=c2, where c is the hypotenuse.
- Basic Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, it divides them proportionally.
- Angle Sum Theorem: The sum of the interior angles of a triangle is always 180 degrees.
How is geometry used in real life?
- Geometry plays a crucial role in various fields:
- Architecture: Designing buildings and structures.
- Engineering: Constructing machines, bridges, and vehicles.
- Computer Graphics: Creating 3D models in video games and movies.
- Navigation: Using GPS systems that rely on geometric algorithms.
- Art and Design: Creating patterns and ensuring symmetry in designs.
How does geometry relate to other branches of mathematics?
- Algebra: Coordinate geometry combines algebra and geometry to study shapes on a plane using equations.
- Trigonometry: Builds on geometric concepts, especially involving angles and triangles.
- Calculus: Involves the study of curves and surfaces, using geometry to calculate areas and volumes.
- Physics: Geometry is essential in understanding forces, motion, and space.
