Bernoulli’s Principle – Definition, Equation, Derivation

Daniel Bernoulli, a prominent mathematician from Switzerland, invented Bernoulli’s Principle, back in the year 1752. According to this principle, the speed of moving liquid is directly proportional to the pressure rise in the moving liquid. This principle is important to verify or find out how various quantities behave especially in a moving fluid that is at a high-speed pace. And here in the article below, we will provide all the answers to your questions about Bernoulli’s principle in much more detail.

What is Bernoulli’s Principle?

Theoretically, it is defined as the total mechanical energy of moving fluid, which consists of the gravitational potential energy of elevation, at which the Kinetic energy and the fluid pressure of moving fluid will remain constant.  Foremost, the Bernoulli Principle states that the horizontal flow or fluid will have low pressure when the speed of moving liquid is slow. While the pressure observed in the high-speed moving liquid is relatively high.

Understanding Bernoulli’s Principle

Fluid Flow: Bernoulli’s Principle applies to the flow of fluids, whether they are liquids or gases, and is particularly relevant in situations where the flow is streamlined and the fluid behaves as an ideal fluid.

Velocity and Pressure: The principle suggests that within a fluid flow, areas of higher fluid velocity correspond to lower pressure, while areas of lower fluid velocity correspond to higher pressure. This inverse relationship between velocity and pressure is a consequence of the conservation of energy within the fluid flow.

Conservation of Energy: Bernoulli’s Principle can be understood in terms of the conservation of energy along a streamline. As fluid flows through a tube or pipe, it exchanges between kinetic energy (associated with the fluid’s velocity), potential energy (associated with the fluid’s height or elevation), and pressure energy.

Energy Conservation Equation: Mathematically, Bernoulli’s Principle is expressed as an energy conservation equation, where the total mechanical energy per unit mass of the fluid remains constant along a streamline:

Mathematically, Bernoulli’s principle is expressed as, 

\(p+ \frac{1}{2} \rho v^{2} +\rho gh=constant\)

Where p = pressure exerted by Fluid 

v = velocity of the fluid 

ρ = density of the fluid 

h = height of the container

Components of Bernoulli’s Theorem

The main components of Bernoulli’s theorem are explained below,

1. Pressure Energy: The pressure energy of a fluid represents the energy associated with the pressure exerted by the fluid on its surroundings. In Bernoulli’s theorem, pressure energy is quantified as P, where P is the pressure exerted by the fluid.
2. Kinetic Energy: Kinetic energy is the energy associated with the motion of the fluid particles. In fluid dynamics, the kinetic energy per unit mass of the fluid is calculated as 1/2where ρ is the density of the fluid and v is the velocity of the fluid.
3. Potential Energy: Potential energy in Bernoulli’s theorem accounts for the gravitational potential energy of the fluid. It is measured as ℎρgh, where g is the acceleration due to gravity and ℎh is the height of the fluid above a reference point.

Bernoulli’s Principle Derivation

Now that you have understood the basics of Bernoulli’s principle. Let us now talk about how to derive Bernoulli’s principle and this is Bernoulli’s theorem derivation.

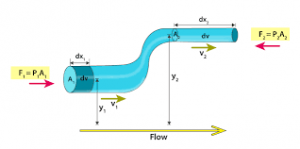
Before we delve into the topic, there are certain things you must keep in mind, such as,  

• The energy flow of the liquid is conserved, because of no presence of viscous forces. 
• The density of incompressible fluid will always remain constant. 

So, firstly, the work done on the fluid is expressed as,

\(dW= F_{1} d x_{1}-F_{2} d x_{2}\)

\(dW= p_{1} A_{1}dx_{1}-p_{2} A_{2}dx_{2} \)

\(dW=p_{1}dv-p_{2}dv=(p_{1}-p_{2})dv\)

From the definition, we can find the change in the Kinetic Energy of the Fluid as,  

\(dK= \frac{1}{2} m_{2} v_{2}^{2}-\frac{1}{2} m_{1} v_{1}^{2}= \frac{1}{2} \rho dv(v_{2}^{2}-v_{1}^{2})\)

Change in Potential Energy is, 

\(dU= m_{2}gy_{2}-m_{1}gy_{1}= \rho dvg( y_{2} -y_{1} )\)

Therefore, the energy equation is given as: 

\(dW=dK+dU\)

And by rearranging the above equation, you will get,  

\(p1+ \frac{1}{2} \rho v_{1}^{2}+ \rho gy1=p2+ \frac{1}{2} \rho v_{2}^{2}+ \rho gy2\)

Principle of Continuity

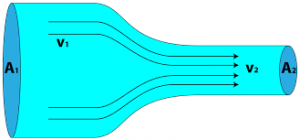
According to the Principle of Continuity, it is, if the fluid is in streamlined flow, and is in-compressible, then the mass of the fluid passing through this, is said to be equal at all cross sections. 

From the above situation, we can say the mass of liquid inside the container remains the same. 

The rate of mass entering = Rate of mass leaving 

The rate of mass entering =\(\rho A_{1} V_{1}\Delta t\)   —> (1)

The rate of mass entering = \(\rho A_{2} V_{2}\Delta t\)   —> (2)

Using the above equations, 

\(\rho A_{1} V_{1}=\rho A_{2} V_{2}\)

By solving the above equation at points 1 and 2, 

We will get the Velocity of efflux as,  

\( v_{2} = \sqrt{2gh} \)

Relation between Conservation of Energy and Bernoulli’s Equation

The relationship between the conservation of energy principle and Bernoulli’s equation is fundamental in understanding fluid dynamics and the behavior of flowing fluids. Bernoulli’s equation, derived from Bernoulli’s theorem, encapsulates the conservation of energy principle as it applies to ideal fluid flow.

Conservation of Energy Principle:

The conservation of energy principle states that the total energy within a closed system remains constant over time, provided that no energy is added to or removed from the system. In the context of fluid dynamics, this principle applies to the various forms of energy present within a flowing fluid, including pressure energy, kinetic energy, and potential energy.

Bernoulli’s Equation:

Bernoulli’s equation is a mathematical expression derived from Bernoulli’s theorem, which describes the conservation of energy along a streamline in ideal fluid flow. It states that the sum of the pressure energy, kinetic energy, and potential energy per unit volume remains constant along the flow path. Mathematically, Bernoulli’s equation can be expressed as:

+1/2+ℎ=constantP+21​ρv2+ρgh=constant

Where:

• P represents the pressure energy,
• ρ denotes the density of the fluid,
• v signifies the velocity of the fluid,
• g denotes the acceleration due to gravity,
• h represents the height of the fluid above a reference point.

Understanding the Relationship

1. Conservation of Energy: The conservation of energy principle asserts that the total mechanical energy within a fluid system remains constant, barring the addition or subtraction of external work.
2. Bernoulli’s Equation: Bernoulli’s equation embodies the conservation of energy principle within fluid flow, stating that the sum of the pressure energy, kinetic energy, and potential energy per unit volume remains constant along a streamline.

Implications and Assumptions

• Bernoulli’s equation assumes ideal fluid behavior, where the fluid is incompressible, non-viscous, and flows along a streamline.
• It also assumes that no external forces are acting on the fluid, such as friction or viscous forces, which would otherwise dissipate energy from the system.

The relationship between the conservation of energy principle and Bernoulli’s equation underscores the fundamental nature of energy conservation in fluid dynamics. By understanding and applying Bernoulli’s equation, engineers and scientists can analyze and predict fluid flow behavior, design efficient fluid systems, and solve practical engineering problems across a wide range of applications.

Applications of Bernoulli’s Principle

Bernoulli’s principle, derived from Bernoulli’s equation, finds numerous applications across various fields due to its ability to explain the relationship between fluid speed and pressure in a flowing fluid. Here’s a detailed exploration of some of the key applications of Bernoulli’s principle:

1. Aerodynamics:

Airplane Wings: Bernoulli’s principle explains the generation of lift in airplane wings. As air flows faster over the curved top surface of the wing compared to the bottom surface, the pressure above the wing decreases, creating lift. This principle is fundamental to the design and operation of aircraft.

2. Hydraulics and Fluid Mechanics:

Pitot Tubes: Used in aircraft and fluid mechanics, pitot tubes utilize Bernoulli’s principle to measure airspeed or fluid flow velocity by comparing the dynamic pressure of the fluid to the static pressure. Pitot tubes are critical instruments for determining airspeed in aviation and flow rate in hydraulic systems.

Venturi Effect: The Venturi effect, observed in constricted fluid flow, is a practical application of Bernoulli’s principle. As the cross-sectional area of a pipe narrows, the fluid velocity increases, leading to a decrease in pressure. This phenomenon is utilized in various applications such as carburetors, where the Venturi effect assists in mixing air and fuel.

3. Medical and Biological Sciences:

Blood Flow Dynamics: Bernoulli’s principle aids in understanding blood flow dynamics in arteries and veins. As blood flows through a constricted vessel, its velocity increases, causing a decrease in pressure according to Bernoulli’s principle. This understanding is crucial for diagnosing and treating cardiovascular conditions.

4. Sports and Recreation:

Curveballs in Baseball: Pitchers in baseball use Bernoulli’s principle to create curveballs. By spinning the ball, they create a difference in air pressure on opposite sides of the ball, causing it to curve during flight. This application of Bernoulli’s principle adds complexity and strategy to the game.

5. Plumbing and Household Appliances:

Spray Nozzles: Bernoulli’s principle is employed in spray nozzles, where high-speed fluid flow causes a pressure drop, allowing for atomization and spraying. This principle is utilized in various household appliances such as showerheads, garden sprayers, and aerosol cans.

6. Weather Phenomena:

Tornado Formation: Bernoulli’s principle plays a role in the formation of tornadoes. As air flows rapidly into a tornado vortex, the pressure decreases due to the increase in velocity, contributing to the low-pressure system characteristic of tornadoes.

In other words, Bernoulli’s principle is a versatile concept with applications spanning aviation, engineering, medicine, sports, and beyond. Its ability to explain fluid behavior in diverse scenarios makes it an invaluable tool for engineers, scientists, and practitioners across various fields. By understanding and harnessing Bernoulli’s principle, we can design efficient systems, improve technologies, and deepen our understanding of fluid dynamics in nature and human-made systems. And these are a few major application of Bernoulli’s theorem.

Conclusion

As you can understand from the above sections, Bernoulli’s principle formula, Bernoulli effect, and various facts about Bernoulli’s Principle, as well as its applications, are very complex, and the students have to study them for a long time in order to memorize them. If you have any similar kind of struggles in these chapters, then we suggest you join coaching classes. And talking about coaching, the Tutoroot platform is offering online interactive classes for students with various benefits. If you are interested, please visit the Tutoroot platform to learn more. 

Frequently Asked Questions

What is Bernoulli’s Theorem?

Bernoulli’s theorem is a fundamental principle in fluid dynamics that states that in a steady flow of an ideal fluid, the sum of pressure energy, kinetic energy, and potential energy per unit volume remains constant along any streamline. In simpler terms, it describes the conservation of energy within a fluid flow, stating that the total mechanical energy per unit mass of the fluid is conserved along the flow path. Bernoulli’s theorem is derived from the principle of conservation of energy applied to fluid flow.

State and Prove Bernoulli’s Theorem

The statement of Bernoulli’s theorem has been provided above. To prove Bernoulli’s theorem, one typically applies the principle of conservation of energy to fluid flow. The proof involves considering a fluid element along a streamline and analyzing the work done by pressure forces, kinetic energy, and potential energy as the fluid moves along the streamline. By accounting for changes in these energy components and their rates of change along the flow path, one can demonstrate that the total mechanical energy per unit mass of the fluid remains constant along the streamline, validating Bernoulli’s theorem.

Applications of Bernoulli’s Theorem

Bernoulli’s theorem finds numerous applications across various fields, including:

Aerofoil Design: In aerodynamics, Bernoulli’s theorem helps explain the generation of lift by airfoils, such as airplane wings, by showing how differences in air pressure create lift.

Pitot Tubes: Used in aircraft to measure airspeed, pitot tubes utilize Bernoulli’s theorem to compare the dynamic pressure of the fluid to the static pressure.

Venturi Effect: Applied in carburetors and water pipes, the Venturi effect uses a constriction in the flow to create a pressure difference, demonstrating Bernoulli’s principle.

Blood Flow: Bernoulli’s theorem explains how the flow of blood through arteries and veins varies with changes in blood vessel diameter and speed.

Spray Nozzles: In spray nozzles, Bernoulli’s principle explains how the high-speed flow of a fluid causes a drop in pressure, allowing for atomization and spraying.

4. State Bernoulli’s principle.

According to this principle, the Total Mechanical energy of moving fluid comprises the gravitational energy of elevation, then the fluid motion and the kinetic energy will remain constant.