Kirchhoff’s Law – Voltage Law, Current Law, Calculation

The students who are studying 11th class will come across circuits and various other related topics in the Current Electricity Chapter. In order to solve most of the problems in these chapters, the candidates must first understand Kirchhoff’s Voltage Law, and Kirchhoff’s Current Law, as well as the formula. Furthermore, Kirchhoff’s Law plays a crucial role in finding various important principles, to calculate various quantities in a circuit.

In this chapter, we shall focus on Kirchhoff’s Laws, further distinguished into:

• Kirchhoff’s Current Law
• Kirchhoff’s Voltage Law

What is Kirchhoff’s Law? 

What is Kirchhoff’s Law?

Kirchhoff’s Law is named after German physicist Gustav Kirchhoff, who developed the two laws that define and determine current and energy conservation in electric circuits. These laws are Kirchhoff’s Current Law and Kirchhoff’s Voltage Law. The Kirchhof’s laws cover every electric circuit and knowledge of their fundamentals is vital in learning about the functioning of electric circuits. Kirchhof’s Laws are most important in measuring the electrical resistance of a complex network or the impedance of an AC. They are also helpful in understanding the flow of current in various networks.

Normally, in order to find resistance and many other quantities, inside two or more resistors connected in parallel or series, Ohm’s law is used. However, this alone cannot be used while trying to find current and voltage in complex circuits like T networks or Bridge.

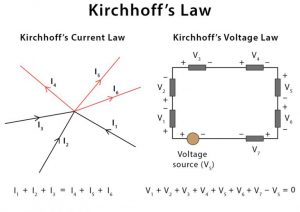
Kirchhoff’s Current Law (KCL)

Kirchhoff’s First Law or the Junction Rule, states that the total number of currents passing through a circuit is similar to the currents flowing outside the junction in a circuit. Moreover, according to this law, the total number of charges entering a node in a circuit will be equal to the charge leaving the node. This in turn means during the passage of current, there is no loss of charge or electricity.

The total current that flows into a junction or a node is equal to the charge that leaves the node, since no charge has been lost.

So, from the first diagram as you can notice, the currents I1, I2, and I3 entering the nodes, which are usually positive, are equal to the negative currents I4, I5, and I6. Which can be specified in an equation, like

I1 + I2 + I3 – I4 – I5 – I6 = 0 

A node is a junction that links multiple current-carrying routes such as cables. Kirchhoff’s current law helps in thorough analysis of parallel circuits. Kirchhoff’s Current Law is applicable only when the total electric charge stays constant inside the circuit. The Current Law is most suited for high-frequency AC circuits.

Kirchhoff’s Voltage Law (KVL)

Like the current law, Kirchoff’s second law is used to find the calculated voltages passing through a circuit. For instance, according to Kirchoff’s second law, the voltage passing through a loop should be equal to the voltage drop occurring in the same loop in a closed circuit. Therefore, by adding each voltage inside the closed circuit will be zero, this principle is generally known as conservation of energy.

From the second diagram, you can spot the different voltages present in a closed circuit. That can be specified as an equation such as,

V1 + V2 + V3 + V4 + V5 + V6 + V7 – Vs = 0 

In short, Kirchhoff’s Voltage Law signifies that the voltage around a loop is equal to the sum of every voltage drop in the same loop for any closed network and will equal zero. This character of Kirchoff’s Law also represents the conservation of energy. This also denotes the algebraic sum of all voltages.

In order to arrive at an accurate outcome, the direction must be maintained in clockwise or anticlockwise.

The function is discharged by electrical charges or on the electrical charges, owing to the presence of the electrical forces inside the component.

The total output from the charge carriers on the rest components will be equal to the total work accomplished on the charge carriers because of electrical forces. Thus, the potential differences across the element are concluded to be equal to zero.

With Kirchhof’s Law, measuring unknown voltages and currents gets easier. In the case of complex closed-loop circuits and their analysis, the eventual simplification becomes manageable.

It must be noted that Kirchhoff’s laws are effective under the hypothesis that there is the absence of fluctuating magnetic fields inside the closed loop. When there is an effect of the fluctuating magnetic field, electric fields and electromotive force could be induced leading to the breaking of Kirchhoff’s rule.

Applications of Kirchhoff’s Laws

Now that you have understood the basics of Kirchoff’s Current and Voltage Law, as well as the Kirchhoff equation. Let us talk about the various applications of these laws. 

• Helps candidates find out the resistance and voltage in each circuit easily. 
• It also helps them to differentiate each voltage and resistance passing through a circuit. 
• Students can find Kirchoff equations for each node. 
• By employing the linear equations from these principles, the individuals will be able to find unknown currents and voltage. 
• They can be used to identify the voltage changes or each voltage in a closed circuit or independent circuit. 

Conclusion

The above article helped you find all the answers to your questions, like state and explain Kirchhoff’s Law, as well as its various applications. So, if you are one of those people who is currently struggling with the Physics subject or specifically the current electricity chapters, as there are a lot of complex principles and laws. Then it would be better for you to join an online interactive class or get a Home Tutor Online. If you are looking for online interactive classes that are low on budget but come with various unique features and benefits, then the Tutoroot platform will be a good option for you. 

Frequently Asked Questions

What are Kirchhoff’s 1st and 2nd laws?

As explained in the above sections, Kirchoff’s first law states that all the current passing through a node inside a circuit should be equal to the current passing out of the node. Whereas the second law states that all the volume inside a closed circuit or independent loop will be equal to zero.

What KCL or Kirchhoff’s Current Law?

Kirchhoff’s Current Law (KCL) or Kirchhoff’s First Law or the Junction Rule states that the total number of currents passing through a circuit is like the currents flowing outside the junction in a circuit

What is KVL or Kirchhoff’s Voltage Law?

Kirchhoff’s Voltage Law (KVL) or Kirchoff’s second law is used to find the calculated voltages passing through a circuit. For instance, according to Kirchoff’s second law, the voltage passing through a loop should be equal to the voltage drop occurring in the same loop in a closed circuit. Therefore, by adding each voltage inside the closed circuit will be zero, this principle is generally known as conservation of energy.