What is Angle? – Types, Examples, Diagrams

What is an angle?

In a straight line when another straight line intersects at a shared terminal, an angle is generated. An angle’s vertex is the common point of contact. Angle is derived from the Latin word angulus, which means “corner.” 

Types of Angles

• Acute angle 
• Obtuse angle 
• Right angle 
• Reflex angle 
• Straight angle 

An acute angle, for example, is one that is less than 90°, whereas an obtuse angle is one that is more than 90°. There are also some unique angle pairings. Let us go through the various sorts of angles in depth. 

Based on Direction

The direction or magnitude of an angle is the rotation around the vertex that causes one of the arms to create an angle. The larger the gap between the arms, the bigger the magnitude. As an example, 

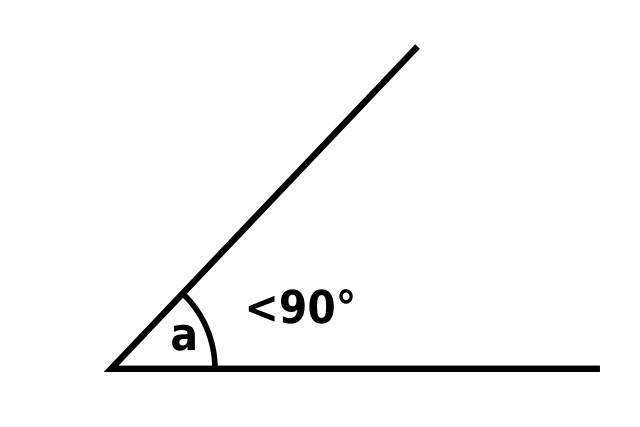
Acute Angle

An acute angle is any angle that is descending from 90°. An acute angle is generated when two rays cross at a vertex and form an angle smaller than 90°. Acute angles include 20°, 30°, 45°, and 60°. Examine the diagram, which indicates that XYZ is an acute angle. 

Right Angle

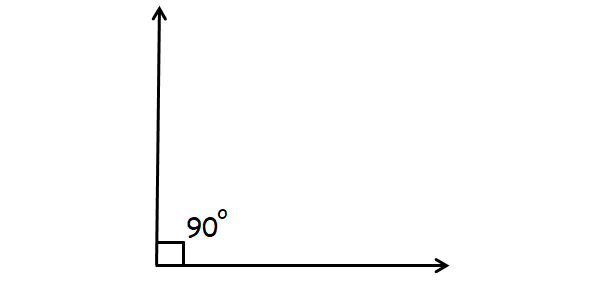
A right angle or 90° angle is generated when the angle formed by two rays is exactly 90°. Look at the diagram, which indicates that AOB is a right angle or a 90° angle. 

Obtuse Angle

Obtuse angles are those that are more than 90° but less than 180°. In the below illustration, the angle created by the lines PQ and QR is obtuse as it includes 110°, 130°, 145°, and 165°. 

Straight Angle

A straight angle is a straight line, as the name implies, and the angle created between two rays is precisely equal to 180°. The two lines are opposite each other at a straight angle. A straight angle is made by joining two adjacent right angles, or two right angles make up a straight angle. In the diagram given below, SRT represents a 180° angle or a straight angle. 

Angle of Reflex

A reflex angle is an angle that is more than 180° but less than 360°. ABC is a reflex angle that includes 210°, 250°, and 310°. 

The angle of Total Rotation

A full rotation angle is generated when one of the angle’s arms completes a full revolution or 360°. MNR = 360° in the figure and is referred to as a complete rotation angle. 

Based on Rotation

The next type of angle is dependent on the rotational direction of angles. Let us look at angle kinds based on rotation. 

Positive Angles

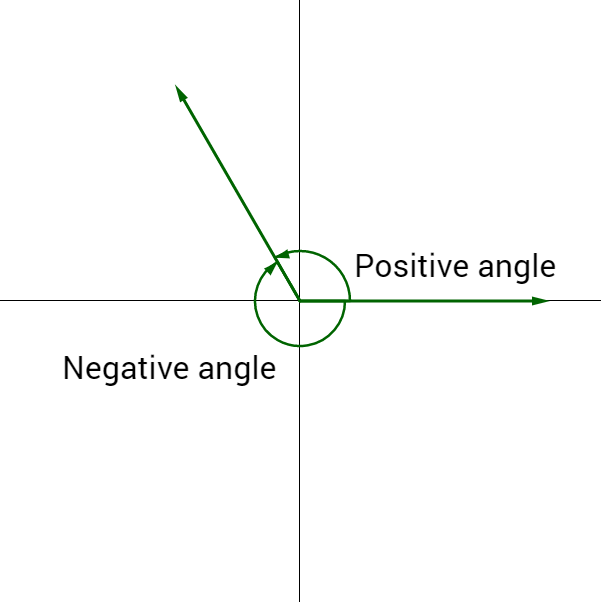
Positive angles are those in which angles are turned counter-clockwise or anti-clockwise from the base. In the diagram below, a positive angle is generated when side 1(AB) is turned anti-clockwise by an angle. 

Negative Angles

Angles that are turned clockwise from the base are considered negative angles. In the diagram below, when side 1 (DE) is rotated clockwise by an angle, a negative angle is generated. 

What is Pair of Angles?

When two lines share a similar terminus, known as a vertex, an angle is produced between them, which is known as a pair of angles. 

Pair of Angle Types

There are different pairs of angles, such as 

Complementary angles

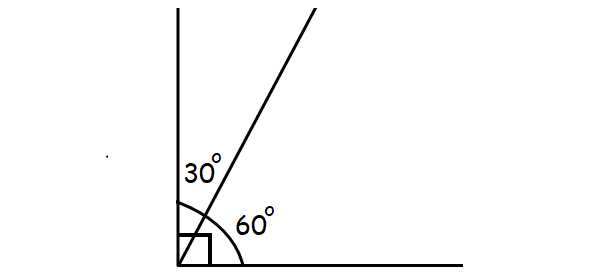
When the total of two angles equals 90°, they are referred to be complementary angles. The two angles can be up to 90°. For instance, the two angles may be 30° and 60°. In this case, one angle is the complement of the other. 

Supplementary angles

When the total of two angles equals 180°, they are referred to as supplementary angles. When the two angles are combined together, they equal 180°. For example, 110° and 70° combine to get 180°. As a result, these two perspectives are considered to be supplementary. In this case, one perspective supplements another. For example, the 60° supplement is (180° – 60°), which equals 120°. 

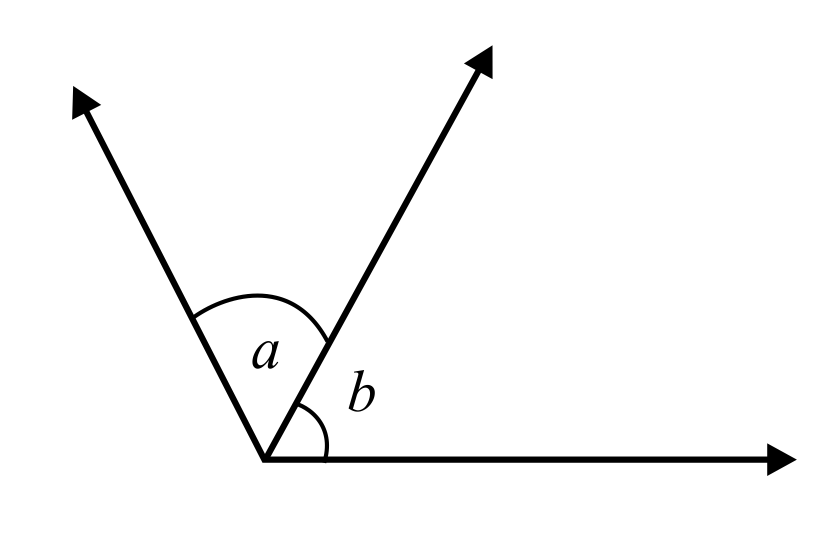
Linear Pair

Linear pairs are formed when the non-common arms of neighboring angles are exactly opposite to each other or extend in the opposite direction. It is obvious that they form a straight line when defined as linear. 

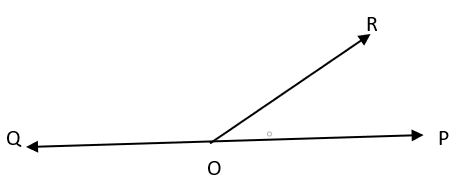
Adjacent angles

When two angles are joined by one common arm and have one common vertex, and the non-common arms are on each side of the same arm, they are referred to as neighboring angles. 

Vertically Opposite angles

When two lines cross, the angles opposite each other are equal and are referred to as vertical angles, also known as vertically opposite angles. 

Final Notes

Understanding angles and the many types of angles will help you solve many difficult problems. Join  Tutoroot’s Maths Online Tuition to get personalized help understanding it completely. 

FAQ’s

How many types of angles are there?
Angles are classified into five categories based on their direction.

What are the Parts of an Angle?
An angle’s components are the vertex and the two arms that form the angle.