What is Bragg’s Law? – Definition, Derivation, Formula
Understanding Bragg’s Law
Bragg’s Law is a fundamental concept in diffraction. In this blog post, we will uncover the incredible secrets behind Bragg’s Law, explore its applications, and delve into its mathematical derivation. Whether you’re just starting your scientific journey or want to deepen your understanding, this comprehensive guide will equip you with the knowledge to unravel the mysteries of Bragg’s Law.
Let’s begin our exploration of Bragg’s Law, where diffraction phenomena take center stage!
What is Bragg’s Law?
Bragg’s Law is a fundamental principle in the field of crystallography that explains the behavior of X-rays and electrons when interacting with crystalline materials. Proposed by William Lawrence Bragg and his father, William Henry Bragg, in 1913, Bragg’s Law opened a new era of scientific inquiry and revolutionized our understanding of crystal structures.
At its core, Bragg’s Law describes the constructive interference between X-rays or electrons and the regularly spaced atomic planes within a crystal lattice. This interference results in the formation of a diffraction pattern, enabling scientists to determine the atomic arrangement and crystallographic properties of materials.
Bragg’s Law Formula
To understand Bragg’s Law, let’s dive into its formula:
The formula for Bragg’s Law is as follows:
nλ = 2d sin(θ)
Where:
- n represents the order of the diffraction peak
- λ denotes the wavelength of the incident radiation
- d is the spacing between adjacent atomic planes
- θ symbolizes the angle of incidence measured concerning the crystal lattice planes
This simple equation encapsulates the fundamental relationship between the diffraction angles, atomic plane spacing, and X-ray or electron wavelengths.
Examples of Bragg’s Law
To gain a practical understanding of Bragg’s Law, let’s explore a couple of illustrative examples:
Example 1: X-ray Diffraction of NaCl Crystal
Suppose we have a sodium chloride (NaCl) crystal excited by X-rays with a wavelength of 1.54 Å. By applying Bragg’s Law, we can determine the angle of incidence, θ, at which constructive interference occurs. Let’s say the atomic plane spacing, d, is 2.82 Å.
Using Bragg’s Law formula:
n * 1.54 Å = 2 * 2.82 Å * sin(θ)
Solving for the angle of incidence, we find that at the first-order diffraction peak (n=1), θ is approximately 20.7 degrees. This specific angle corresponds to the crystallographic planes allowing constructive interference for the given X-ray wavelength and atomic spacing.
Example 2: Electron Diffraction in a Graphene Crystal
Now let’s consider a different scenario involving electron diffraction in a graphene crystal. Suppose we have electrons with a de Broglie wavelength of 0.5 nm incident on the crystal. The atomic plane spacing, d, in the graphene crystal is approximately 0.213 nm.
Based on Bragg’s Law:
n * 0.5 nm = 2 * 0.213 nm * sin(θ)
Calculating the angle of incidence, we discover that at the second-order diffraction peak (n=2), θ is approximately 32.7 degrees. This angle represents the conditions for constructive interference in the graphene crystal, allowing scientists to probe its atomic structure.
These examples demonstrate how Bragg’s Law enables the determination of atomic arrangements and crystal structures through diffraction patterns.
Bragg’s Law Diagram
Let’s visualize the concepts of Bragg’s Law and diffraction with the help of a diagram:
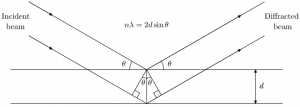
In the diagram, incident waves (represented by red rays) encounter a crystal lattice, with regularly spaced atomic planes shown as parallel lines. As the incident waves interact with the crystal, they undergo diffraction. The diffracted waves (shown as blue rays) emerge at specific angles, following Bragg’s Law, indicating constructive interference and revealing information about the crystal structure.
This diagram provides a visual representation of Bragg’s Law in action, showcasing how diffraction allows researchers to uncover the invisible world of crystalline arrangements.
Bragg’s Law Derivation
Now, let’s dive deeper into the mathematical derivation of Bragg’s Law. Understanding the derivation provides valuable insights into the underlying principles and sheds light on the intriguing connection between mathematics and diffraction phenomena.
The derivation utilizes concepts from wave interference and the geometry of crystal lattices. By considering a set of parallel atomic planes and applying constructive interference conditions, scientists derived Bragg’s Law equation. While the full mathematical derivation is beyond the scope of this blog post, studying it paves the way for a deeper appreciation of the principles governing diffraction.
From the diagram,
nλ = AB + BC
We know that AB = BC, then
nλ = 2AB (Assume it as equation 1)
d is the hypotenuse of the right triangle Abz. Ab is the opposite of the angle θ.
AB = d sinθ (Assume it as equation 2)
Substituting equation 2 in equation 1
nλ = 2d sinθ
Applications of Bragg’s Law
The applications of Bragg’s Law are widespread and extend across numerous scientific disciplines. Let’s explore some of the notable applications:
X-ray Crystallography
Bragg’s Law lies at the heart of X-ray crystallography, a technique extensively used to determine atomic structures of molecules and crystals. By analyzing the diffraction patterns produced when X-rays interact with a crystal, scientists gain invaluable insights into materials’ composition, arrangement, and functional properties. This technique has been pivotal in revealing the structures of complex molecules, including DNA and proteins, leading to groundbreaking discoveries in fields like medicine, chemistry, and biology.
Electron Microscopy
In electron microscopy, Bragg’s Law finds application in electron diffraction experiments. By using a focused electron beam instead of X-rays, researchers can probe the crystallographic properties of materials at the atomic level. Electron diffraction has been instrumental in investigating the structures of nanoparticles, thin films, and various crystalline materials, contributing to advancements in materials science and nanotechnology.
Material Characterization
Bragg’s Law plays a crucial role in material characterization techniques such as powder X-ray diffraction and neutron diffraction. These techniques provide valuable information about the crystal structures, phase compositions, and mechanical properties of materials. By leveraging Bragg’s Law, scientists can identify and analyze different crystal phases, determine the degree of crystallinity, and gain insights into material behavior under various conditions, fostering advancements in materials engineering and research.
These applications represent just a glimpse of the immense impact and versatility of Bragg’s Law in diverse scientific fields, empowering researchers to push the boundaries of knowledge and innovation.
What is Bragg’s Law of Diffraction?
Bragg’s Law of Diffraction is another term often used interchangeably with Bragg’s Law. The concept underlying both terms remains the same – the phenomenon of constructive interference in diffraction patterns due to the interaction between waves and a crystal lattice. These interchangeable terms highlight the diffraction aspect of the law, emphasizing the key role diffraction plays in understanding the inner workings of crystalline materials.
The Concept of Bragg’s Law of Diffraction
To fully grasp the concept of Bragg’s Law of Diffraction, it is crucial to understand diffraction itself. Diffraction refers to the bending or spreading of waves around obstacles or through small openings. When waves interact with a crystal lattice, they experience diffraction, leading to the formation of distinctive patterns. Bragg’s Law of Diffraction provides the mathematical framework to explain and predict the angles at which constructive interference occurs, enabling scientists to decode the messages hidden within diffraction patterns.
Final Notes
Congratulations on completing this deep dive into the captivating world of Bragg’s Law! Armed with a solid understanding of its definition, derivation, and formula, as well as its applications and significance in diffraction phenomena, you are better equipped to explore the vast scientific landscape where Bragg’s Law plays a pivotal role.
Remember, Bragg’s Law is not just a mathematical equation; it is a powerful tool that enables scientists to unlock the secrets of atoms and molecules, revealing the wonders of the microscopic world. So, keep exploring, keep experimenting, and keep unraveling the mysteries that Bragg’s Law helps uncover. Happy discovering!
Are you keen on effortlessly understanding concepts, similar to the explanation provided above? Dive into our Tutoroot Blog section for simplified learning. Enhance your comprehension of subjects and have your doubts cleared through Tutoroot’s physics online tuition. Try out Tutoroot’s online home tuitions today by scheduling a FREE DEMO session.
FAQs
State Bragg’s Law
Bragg’s Law is a scientific principle that helps researchers understand how X-rays interact with crystals. It is expressed by the formula: nλ = 2d sinθ, where nλ is the X-ray wavelength, d is the distance between atomic layers in a crystal, and θ is the angle of X-ray reflection.
State Bragg’s Diffraction
Bragg’s diffraction refers to the phenomenon where X-rays, when incident on a crystal, scatter in a way that creates a distinct diffraction pattern. This pattern is governed by Bragg’s Law and helps scientists analyze the atomic structure of crystals.
Define Bragg’s Law of X-ray Diffraction
Bragg’s Law of X-ray diffraction is a scientific principle that relates the angle of X-ray reflection, the wavelength of X-rays, and the distance between atomic layers in a crystal. It is a crucial tool for determining the structure of crystalline materials.
What is Bragg’s X-ray Diffraction Principle?
Bragg’s X-ray diffraction principle is a fundamental concept in crystallography. It states that when X-rays strike a crystal, they produce a diffraction pattern based on the arrangement of atoms in the crystal lattice. Bragg’s Law is used to interpret this pattern and unveil the crystal’s structure.
