State and Prove Parallel Axis and Perpendicular Axis Theorems
Let’s study the Parallel and perpendicular axes theorem, how to use the perpendicular axis theorem, and how to utilize the parallel axis theorem.
The parallel axis theorem calculates the moment of inertia of a rigid body around an axis parallel to the mass of the object line (about which the moment of inertia is known). The perpendicular axis theorem states that a rigid body’s moment of inertia along an axis that is perpendicular to two other axes about which its moment of inertia is known as equal to the sum of the rigid body’s moments of inertia about the two known axes.
What is Parallel Axis Theorem?
The sum of the moments of inertia of a body about an axis passing through its center and the product of the mass of the body times the square of the distance between the two axes is called the theorem of parallel axis.
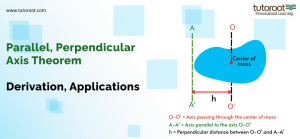
Parallel Axis Theorem Formula
The parallel axis theorem formula is
\(I= I_{c} +M h^{2}\)
Here,
I – a moment of inertia of the body
\(I_{c}\) – moment of inertia around the centre
m – mass of the body
\(h^{2}\) – square distance between the two axes
Derivation of Parallel Axis Theorem
Let Ic be the moment of inertia of an axis passing through the center of mass AB, and I be the moment of inertia around the axis A’B’ at h.
Imagine a particle with mass m at a distance r from the body’s center of gravity.
The distance from A’B’ is thus equal to r + h.
\(I= \Sigma m (r+h)^{2}\)
\(I= \Sigma m( r^{2} + h^{2}+2rh )\)
\(I= \Sigma m r^{2} + \Sigma m h^{2} +\Sigma2mrh\)
\(I=I_{c}+h2 \Sigma m+2h \Sigma mr\)
\(I=I_{c}+M h^{2} +0\)
\(I=I_{c}+M h^{2}\)
What is Perpendicular Axis Theorem?
This theorem only applies to flat bodies. Bodies that are flat and have very little or no thickness. The moment of inertia of a planar body at an axis perpendicular to its plane is equal to the sum of its moments of inertia along two perpendicular axes coincident with the perpendicular axis and situated in the plane of the body.
The formula of the Perpendicular Axis Theorem
When the body is symmetric around two of the three axes, the perpendicular axis theorem is utilized. If you know the moment of inertia about two of the axes, you can calculate the moment of inertia about the third axis using the expression:
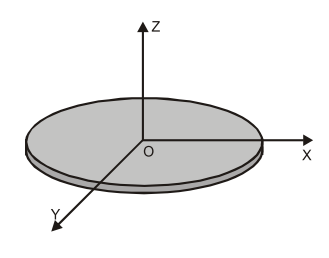
\(I_{z} = I_{x} + I_{y}\)
The axes x, y, and z (which intersect at origin O) are oriented so that the body is in the xy plane, and the z-axis is perpendicular to the plane of the body. Let IX, IY, and IZ denote the moment of inertia around axes X, Y, and Z, respectively.
Example of Perpendicular theorem
Assume we wish to calculate the moment of inertia of a uniform piece of paper as a function of its diameter. Let MR2/2 be its midpoint, where M represents mass and R represents radius. Iz=Ix+Iy as a result of the perpendicular axes theorem. Because the paper is consistent, all of the diameters are the same.
\(I_{x}= I_{y}\)
\(I_{z}=2 I_{x}\)
\(I_{z}=\frac{M r^{2} }{4}\)
Finally, the moment of inertia of a disc about any of its diameters is equal to \(\frac{M r^{2} }{4}\)
Applications of Parallel & Perpendicular Axis Theorems
- The moment of inertia of a rigid body around any axis is computed by combining the parallel and perpendicular axis theorems. The parallel and perpendicular axis theorems may be used to compute the moment of inertia of any spinning object.
- The perpendicular axis theorem calculates the moment of inertia about the third axis.
- The perpendicular axis theorem calculates the moment of inertia of three-dimensional objects.
Final Notes
Are you struggling to keep up with the concepts in your Physics class? Online coaching might be a great option for you. Tutoroot offers interactive online classes that can help you better understand the concepts. Join today!
FAQ
State parallel axis theorem.
The theorem of the parallel axis is the sum of the moments of inertia of a body about an axis passing through its center and the product of the mass of the body times the square of the distance between the two axes.
